Understanding and Improving Convolutional Neural Networks

1. Abstract

딥러닝 프레임워크를 사용하지 않고 C++로 초기 합성곱 신경망인 LeNet-5를 구현했다. 단순한 구현에 집중하기보다 신경망의 기본 요소(활성함수, 목적함수, 경사하강법, 가중치 초기화 방법)가 어떤 원리로 작동하는지 학습하는 데 중점을 두었다. 또한 LeNet-5의 네 가지 문제(기울기 소실, 느린 학습 속도, 공변량 시프트, 과대적합)를 파악하고 해결방안을 제시했다. 개선된 LeNet-5는 MNIST 테스트 데이터를 기준으로 분류 정확도 99.22%를 기록했다. [source]

2. Overall architecture

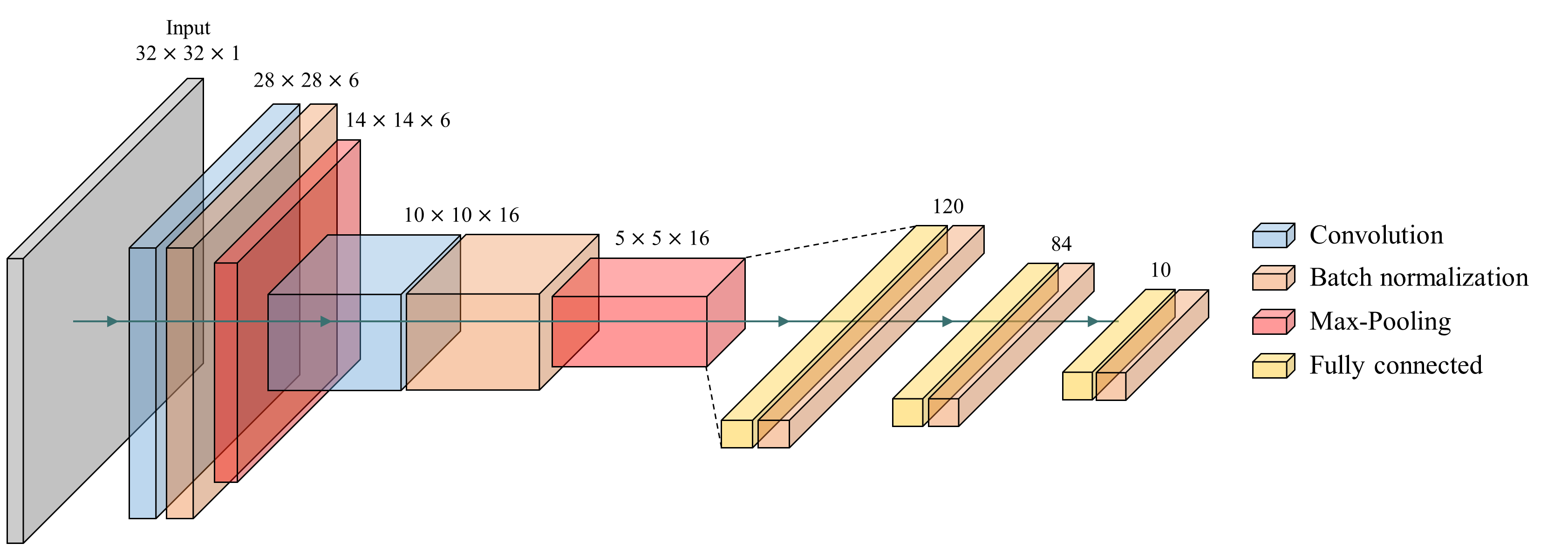
그림 1 개선된 LeNet-5의 전체 구조. 기존 모델의 구조를 그대로 따르되, 합성곱층과 완전연결층 뒤에 배치정규화층을 추가했다. 은닉층의 활성함수를 하이퍼볼릭 탄젠트에서 ReLU로 변경했으며, 출력층에서는 소프트맥스를 사용했다. 목적함수는 평균제곱오차에서 교차 엔트로피로 변경했다.

3. Problems

3.1. Vanishing gradient

기울기 소실은 오차 역전파 과정에서 입력층에 가까워질수록 기울기 크기가 점진적으로 감소하는 현상을 말한다. LeNet-5가 사용하는 하이퍼볼릭 탄젠트 함수는 이 문제에 취약하다. 오차 역전파 알고리즘의 특성상 최초의 기울기에 활성함수의 도함숫값을 지속적으로 곱하게 되는데, 하이퍼볼릭 탄젠트의 도함숫값은 입력값 $x$가 조금만 작거나 커도 0에 수렴하기 때문이다.

3.2. Slow learning

평균제곱오차는 시그모이드 함수와 함께 사용하면 신경망의 학습 속도를 더디게 한다. 학습 중 기울기의 크기에 비례하여 파라미터가 갱신되는데, 평균제곱오차는 오류가 클수록 기울기의 크기를 줄이기 때문이다. 이는 기울기를 구할 때 활성함숫값을 함께 곱하여 발생하는 현상이다. 목적함수를 $x$, 정답 레이블(label) 벡터를 $y$, 신경망의 최종 출력 벡터를 $\hat{y}$, $l$번째 층의 가중치 행렬과 입력 벡터의 곱을 $z^l$, 활성함수를 $\sigma(z)$로 나타낸다고 하자. 이때 $l$번째 층의 기울기

\[\begin{align} \delta^l &= \frac{\partial J}{\partial \hat{y}} \cdot \frac{\hat{y}}{z^l} \\ &= \underbrace{-(y-\hat{y})}_{1} \odot \underbrace{\sigma'(z^l)}_{2} \end{align}\]

이다. $y=[0]$일 때 마지막 줄의 1번과 2번 식이 $\hat{y}$에 따라 어떻게 변화하는지 그래프로 나타내면 아래와 같다. 1번 값은 오차의 크기에 비례하여 증가하나, 2번 값은 $\hat{y}=0.5$를 기점으로 감소한다. 이에 따라 최종 기울기가 오차의 크기에 비례하여 증가하지 못하고 $\hat{y}=0.7$을 기점으로 감소한다.

그림 2 출력층에서 평균오차제곱 목적함수의 기울기가 감소하는 과정.

3.3. Covariate shift

공변량 시프트는 이전 층의 파라미터 값이 갱신됨에 따라 현재 층의 입력값의 분포가 달라지는 현상을 말한다. 가장 간단한 해결법은 각 층의 입력값을 평균이 0이고 표준편차가 1이 되게끔 정규화하는 것이다. 하지만 분포의 중심을 0으로 옮기는 것만으로 편향 항(bias term)이 사라진다. 예를 들어 가중치 행렬과 입력 벡터의 곱 $z=w \cdot x + b$라 하자. 이 분포의 중심을 0으로 옮기면 $\tilde{z}=w \cdot x + \cancel{b} - E[w \cdot x + \cancel{b}]$이 되면서 편향 항이 사라진다.또한 시그모이드나 하이퍼볼릭 탄젠트는 $x=0$ 부근에서 선형함수에 가깝기 때문에 활성함수의 비선형성을 상쇄할 수도 있다.

이러한 문제를 해결하기 위해 배치 정규화는 아래와 같이 정의한다.

\[\tilde{z_i} = \gamma \cdot \frac{z_i - \mu_B}{\sqrt{\sigma^2_B + \epsilon}} + \beta \quad \text{for} \ B=\{z_1, \dots, z_m\}\]

$\gamma, \beta$는 학습 가능한 파라미터이고 각각 스케일(scale), 시프트(shift) 변환을 수행한다. 이때 $\beta$가 편향 항의 역할을 하기 때문에 앞서 언급한 첫 번째 문제를 해결할 수 있다. 또한 $\gamma=\sigma_B, \beta = \mu_B$이면, 입력값을 정규화하기 전의 상태로 복원하기에 두 번째 문제에서도 자유로워진다.

4. Experimental results

Model	Activation (hidden layer)	Activation (output layer)	BatchNorm?	Loss	Error(%)
LeNet-5	Tanh	Sigmoid		MSE	1.06(0.04)
LeNet-5+	ReLU	Softmax		Cross Entropy	0.96(0.06)
LeNet-5++	ReLU	Softmax	$\checkmark$	Cross Entropy	0.78($\pm$0.06)

표 1 MNIST test 데이터셋에 대한 성능 측정 결과. 우측의 오류율은 다섯 번 측정의 평균값이다. 학습률은 0.02, 배치 크기는 32, 에포크(epoch)는 30으로 세 모델 모두 동일하다.

실험에 사용된 모델은 세 가지이다. 첫 번째 모델은 기존의 LeNet-5와 동일하다. 두 번째 모델은 은닉층의 활성함수를 ReLU로, 출력층의 활성함수를 소프트맥스 함수로, 그리고 목적함수를 교차 엔트로피로 변경했다. 마지막 모델은 두 번째 모델에 배치정규화층을 추가했다(그림 1). 실험 결과 LeNet-5+, LeNet-5++는 기존의 모델보다 오류율이 각각 0.1%, 0.28% 감소했다.

4.1. Vanishing gradient: Tanh vs ReLU

ReLU의 도함수는 0 또는 1의 값만 갖는다. 이에 따라 상위 층에서 흘러온 기울기에 도함숫값을 곱해도 그것의 크기가 감소하지 않는다. 물론 도함숫값이 0일 경우 해당 노드의 기울기가 완전히 사라진다. 하지만 이런 희소(sparse)한 특성이 오히려 분류 정확도를 높인다는 것이 실험적으로 확인되었다(Glorot et al., 2011). 기울기 소실 문제가 실제로 완화되는지 확인하기 위해 활성함수를 하이퍼볼릭 탄젠트에서 ReLU로 변경 후, 학습 과정에서 각 층에 흘러온 기울기 크기를 측정했다.

그림 3 신경망 전체 층의 기울기의 크기를 합한 값 $\sum_{i=1}^{n} \lVert \delta^i \rVert_2$ 에서 각 층의 기울기의 크기 $\lVert \delta^l \rVert_2$ 이 차지하는 비율. 만약 기울기가 전혀 소실되지 않았다면 각 비율이 서로 동일해야 한다.

하이퍼볼릭탄젠트를 활성함수로 사용할 때 학습 초기에 기울기가 소실됐다. 그림 3의 좌측 그래프에서 보듯이 상위 층(fc3)에서 하위 층(conv1)으로 갈수록 전체에서 자치하는 비율이 점차 작아진다. 하지만 파라미터를 학습하면서 이러한 현상이 사라졌다. 한편 ReLU로 활성함수를 변경했을 때도 학습 초기에 기울기 소실이 발생했으나 이전보다 더 빠르게 이 현상이 완화되었다.

4.2. Slow learning: MSE vs Cross Entropy

교차 엔트로피를 사용하면 신경망의 느린 학습 속도를 개선할 수 있다. 활성함수와 목적함수로 각각 소프트맥스와 교차 엔트로피를 사용한다고 할 때, $l$번째 층(출력층)의 기울기

\[\delta^l = \sigma(z^l) - y\]

이다. 이때 $y$는 정답에 해당하는 원소만 값이 1인 원-핫(one-hot) 벡터이다. 평균제곱오차와 달리 활성함수의 도함수를 곱하지 않기 때문에 기울기의 크기가 감소하지 않는다. 또한 소프트맥스의 출력값 중 정답 클래스에 상응하는 값에서만 1을 빼면 되기 때문에 연산 속도 면에서도 유리하다. 실험 결과 교차 엔트로피를 사용한 LeNet-5+가 LeNet-5보다 더 빠르게 학습되었다(그림 4).

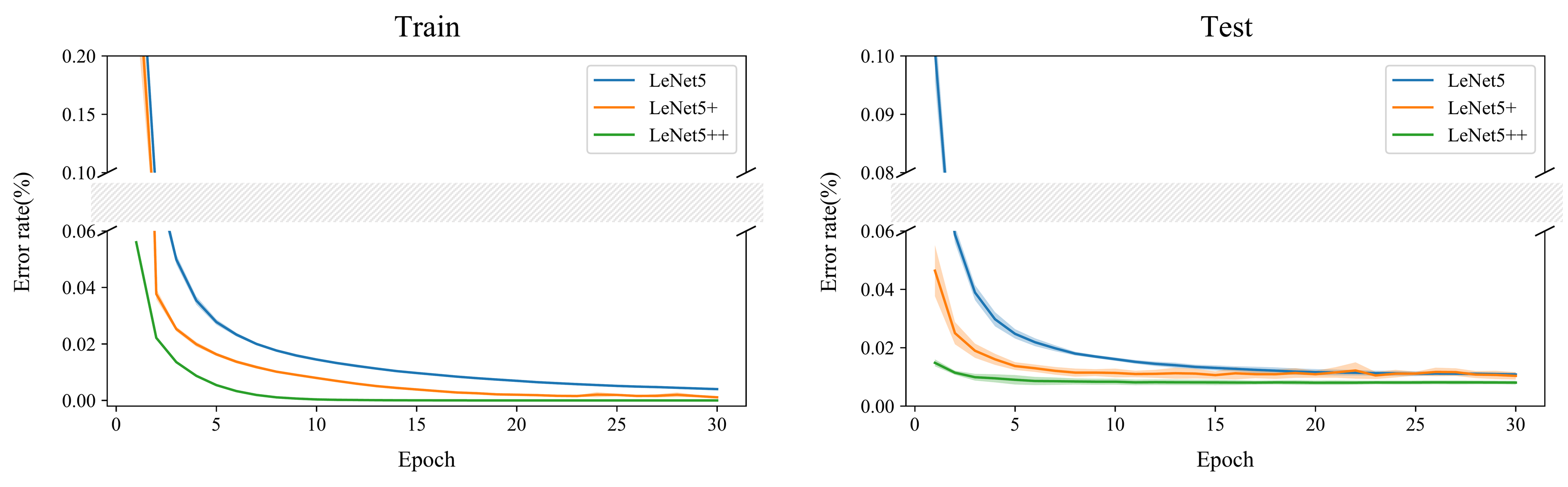
그림 4 LeNet-5, LeNet-5+, LeNet-5++의 학습 중 측정한 오류율의 변화. 진한 선은 다섯 번 측정한 오류율의 평균값을 나타낸다. 그 주위의 반투명한 영역은 표준편차 구간을 나타낸다.

4.3. Covariate shift

공변량 시프트 현상이 존재하는지 확인하고 배치 정규화가 이 현상을 완화시키는지 관찰하기 위해 매 에포크마다 각 층의 활성함수에 입력되는 값을 기록했다. 아래 그림의 첫 행에서 보듯이 배치 정규화를 적용하지 않은 모델의 경우 학습이 진행될수록 각 분포의 표준편차가 증가했다. 이에 비해 배치 정규화를 적용한 모델은 학습 기간 동안 분포의 모양이 일정하게 유지되었다.

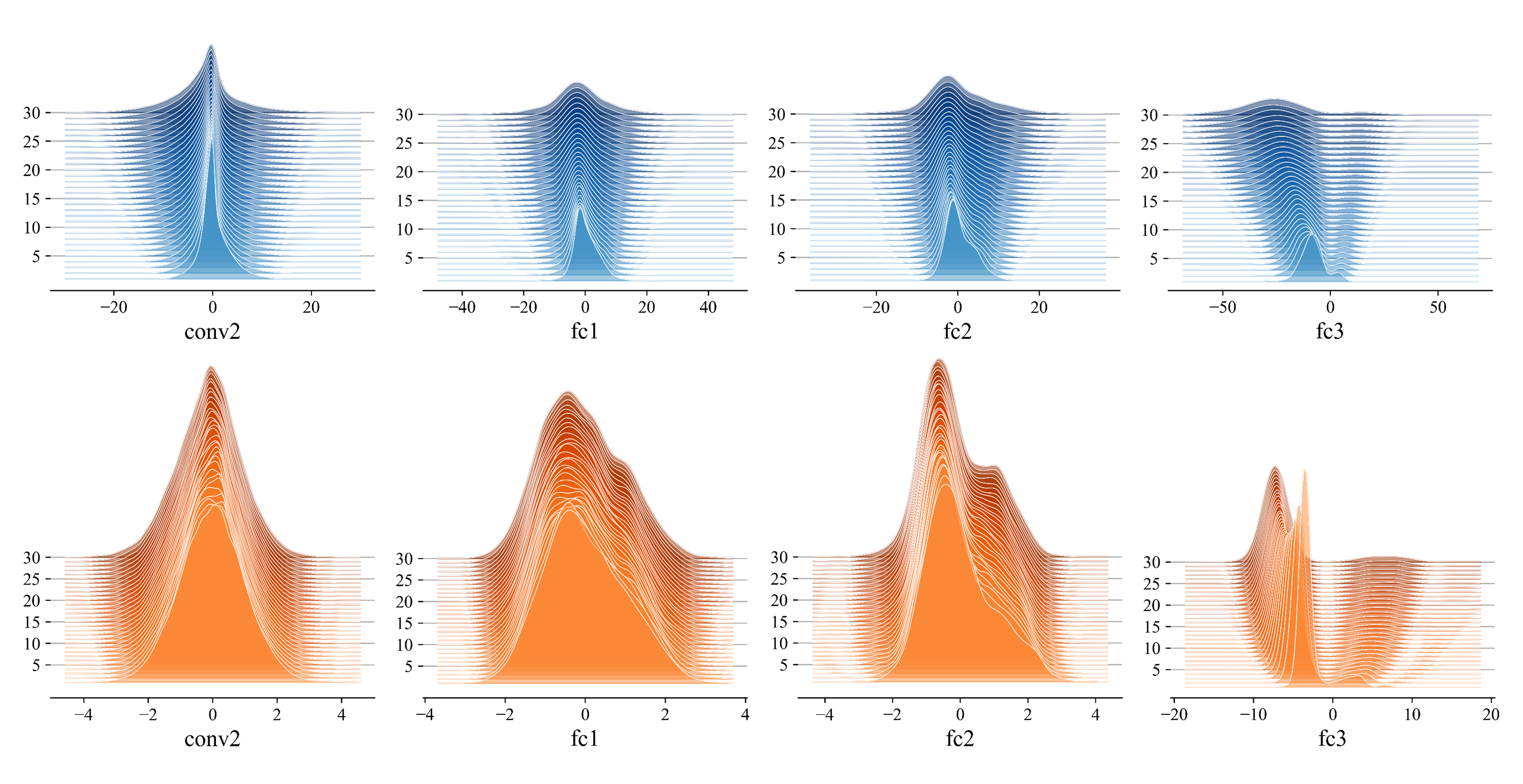
그림 5 활성함수 입력값의 분포. 1행: LeNet-5+(배치정규화 미적용), 2행: LeNet-5++(배치정규화 적용).